ケプラーの第3法則:調和の法則を語る。
ケプラーの第3法則とは
ケプラーの3法則のうち、3番目の法則がケプラーの第3法則だ。
調和の法則ともいう。
| 第1法則 楕円軌道の法則 | 惑星の軌道は太陽をひとつの焦点とする楕円である。 |
| 第2法則 面積速度一定の法則 | 惑星と太陽とを結ぶ直線が一定時間につくる面積は、常に一定である。 |
| 第3法則 調和の法則 | 惑星の公転周期の2乗は、軌道の長半径の3乗に比例する。 |
そもそも軌道の長半径とは
楕円のサイズは長半径と短半径で示す
真円なら中心と円周との距離はどこも同じなので、真円のサイズを表すのに半径は分かりやすい。
ところが、楕円になると中心と円周との距離は場所によって違う。
そこで楕円のサイズは長半径と短半径の二つの半径で示せばいい。
楕円の中で最も長い半径が長半径、最も短い半径が短半径だ。
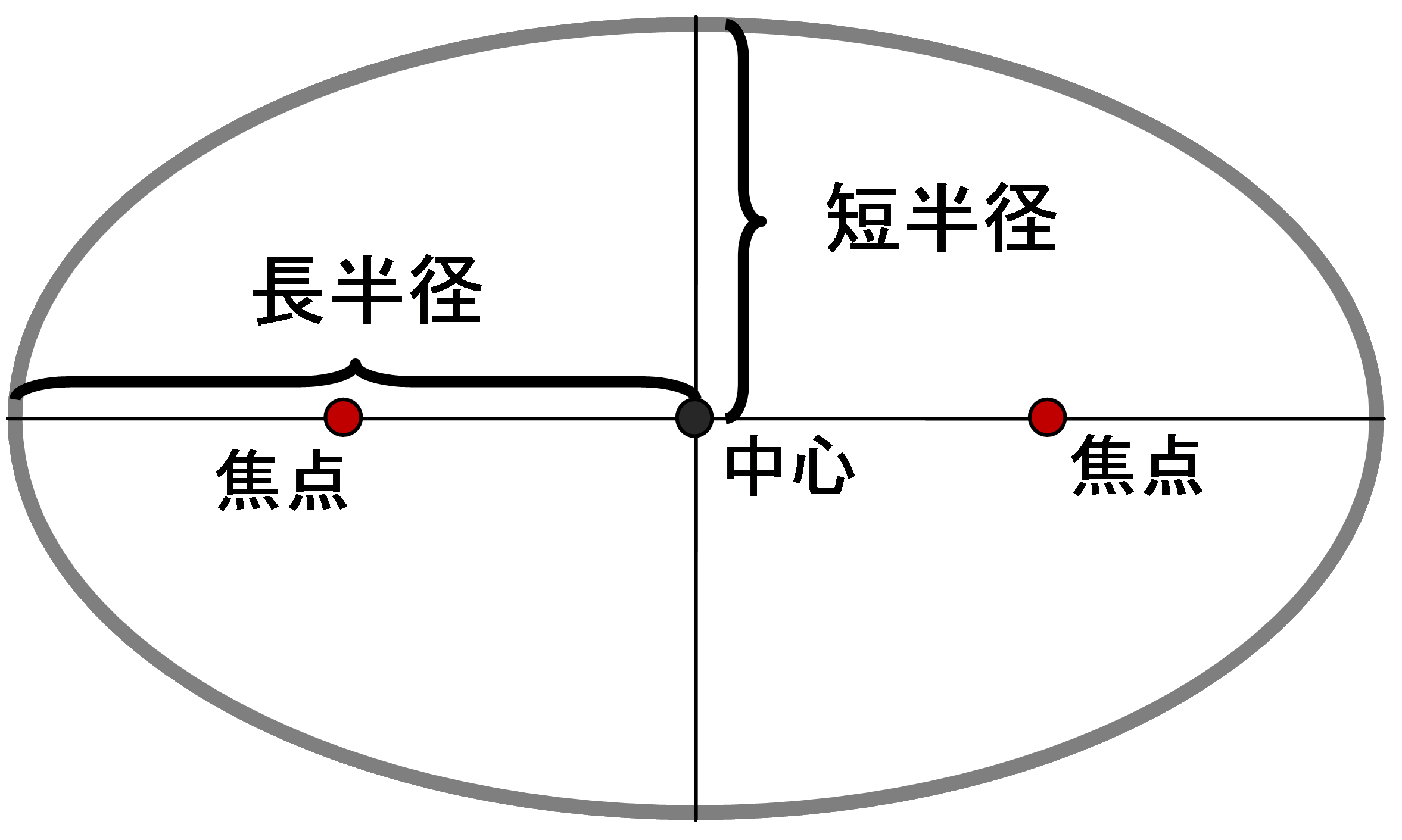
焦点は必ず長半径上にあるのも、楕円の特徴だ。
なぜ調和の法則というのか?
天文年鑑で各惑星の軌道長半径と公転周期を調べると次の表になる。
| 惑星 | 軌道長半径 | 公転周期 |
| 水星 | 0.38710 | 0.240852 |
| 金星 | 0.72333 | 0.615207 |
| 地球 | 1.00000 | 1.000040 |
| 火星 | 1.52368 | 1.880866 |
| 木星 | 5.20260 | 11.86155 |
| 土星 | 9.55491 | 29.53216 |
| 天王星 | 19.21845 | 84.25301 |
| 海王星 | 30.11039 | 165.2269 |
出典:天文年鑑2015年版,誠文堂新光社
軌道長半径の3乗と公転周期の2乗を計算すると次の表になる。
| 惑星 | 軌道長半径 | (軌道長半径)3 | 公転周期 | (公転周期)2 |
| 水星 | 0.38710 | 0.05801 | 0.240852 | 0.05801 |
| 金星 | 0.72333 | 0.37845 | 0.615207 | 0.37848 |
| 地球 | 1.00000 | 1.00000 | 1.000040 | 1.00008 |
| 火星 | 1.52368 | 3.53738 | 1.880866 | 3.53766 |
| 木星 | 5.20260 | 140.81902 | 11.86155 | 140.69637 |
| 土星 | 9.55491 | 872.32798 | 29.53216 | 872.14847 |
| 天王星 | 19.21845 | 7098.31184 | 84.25301 | 7098.56969 |
| 海王星 | 30.11039 | 27299.15108 | 165.2269 | 27299.92848 |
出典:天文年鑑2015年版,誠文堂新光社を利用。計算は織野。
軌道長半径の3乗と公転周期の2乗をグラフにすると下図になる。
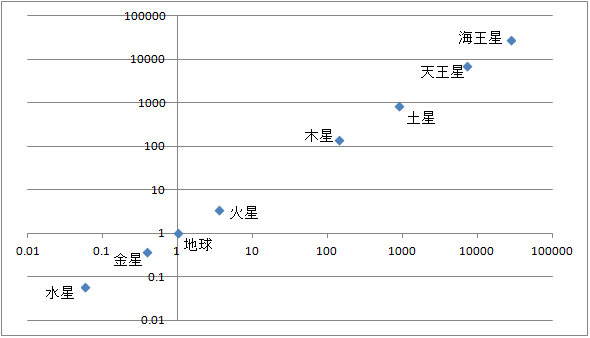
各惑星の軌道長半径と公転周期は無関係に見えたかもしれないが、すべての惑星のプロットが直線上に並び、見事に調和がとれていることが分かる。
だから調和の法則というのだ。
真円に近い楕円軌道でも、極端につぶれた楕円軌道でも長半径が同じなら、公転周期も同じになる。
スポンサーリンク
参考文献・サイト
国立天文台
Kepler's Three Laws of Planetary Motion
天文年鑑2015年版,誠文堂新光社
2015/09/29